
前言
随着OpenAI开源了首个原生态支持FP4格式的GPT-OSS系列大模型,AI领域也正式跨入了低精度计算的时代。当前,主流大模型的规模已经越来越大,需要容量更大且计算力更强的硬件来支撑其训练和推理。而低精度量化则是一种能大幅提升计算效率的手段。本文将由浅入深介绍低精度量化的原理,以及学术界业界对低精度训练的最新探索。
在当下的AI潮流,大模型需要越来越多的硬件,例如GPGPU芯片,来支撑其训练和推理的计算。其主要计算是由海量的矩阵乘法操作所组成。即便目前的硬件已经具备越来越强悍的矩阵乘法处理器,例如张量核(Tensor Core),也难以满足大模型那惊人的矩阵乘法计算量。此外,大模型的计算还需要对大量的数据进行储存,远超过目前硬件的储存单元,例如HBM,所能承载容量。数据的搬运也同样是个问题,无论是对不同硬件之间的传输,还是在硬件内部不同层级的储存单元中的搬运,对带宽的压力都几乎达到了极限。
针对大模型规模的不断扩大,存在一种简单的方法,能够同时有效应对计算量大、储存不足和数据传输慢这三个问题,也就是模型低精度量化;其作用为将模型的权重和中间变量进行低精度截断,从而大幅压缩数据量,并利用硬件中专门的低精度矩阵乘法处理器来加速计算。
目前,硬件上已逐渐开始支持各种低精度的格式(FP8、FP4等)以及对应的低精度矩阵乘法计算。因此,如何在极低精度的环境下保证模型量化所造成的误差不会过度影响模型本身的能力也就成为业界和学术界所面临的一大挑战。目前,DeepSeek V3/R1、Kimi-K2等主流开源大模型均原生态支持了FP8的低精度格式,以及OpenAI最新开源的GPT-OSS系列模型在混合专家(MoE)层也已经原生态支持了MXFP4这种细粒度的低精度格式,代表了低精度量化在未来AI领域中的重要性。
为何模型需要做低精度量化?
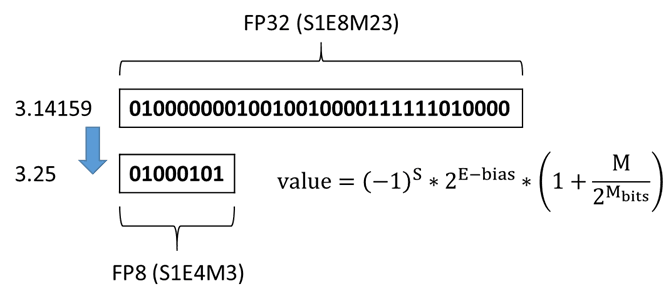
3.14159这一数字从高精度格式(FP32)转换到低精度格式(FP8),内存空间占用节省了4倍(从32个比特到8个比特)。信息量的降低也意味着计算量的减少。
我们主要从三点展开。
首先,低精度量化带来的最直接好处就是减少内存占用,例如GPGPU里的HBM容量有限,然而模型运算时所占用的内存却很大,包括模型权重、中间变量、推理时需要保存每层的KV Cache、训练时需要保存的Master权重、一阶/二阶优化器状态等,均对HBM的容量带来巨大压力。虽现有技术可以使用CPU-offload这类技术来扩展总容量,然而这会带来很高的延迟。低精度量化则可以直接对模型中的数据(权重、中间变量、KV Cache等)进行2倍、4倍甚至更高倍率的压缩,带来极为可观的收益。
其次,低精度量化所带来的数据量减小可以加快传输,降低带宽需求和延迟。这里的数据传输包括在芯片内部不同层级的内存之间(HBM、L2缓存、共享内存、寄存器、张量核缓存等),以及在芯片外部之间的连接,例如南向scale-up节点内互联与北向scale-out节点外互联。在大模型的场景中,数据传输与计算同样重要。在模型训练时,因为通常使用不同芯片处理不同的批量数据,因此需要传输不同批量的梯度进行累加,从而更新模型权重。而在模型推理时,注意力机制的计算通常呈现出memory-bound的情况(存在矩阵-向量乘法以及KV Cache的读取,DeepSeek V2中引入的MLA结构 [1] 可缓解该问题),需要频繁地在不同层级内存中读写数据,对带宽要求极高。无论在模型训练还是推理中,都很有可能需要做分布式计算,包括数据并行(DP)、张量并行(TP)、序列并行(SP)、流水并行(PP)、MoE大模型特有的专家并行(EP)以及这些并行策略的各种组合,需要在不同芯片中反复读写数据。而低精度数据则极大缓解了这些性能问题。
最后,低精度格式的计算,尤其是低精度矩阵乘法已逐渐被现代芯片所支持,包括FP8和FP4格式。低精度运算的面积和功耗成本都更低,芯片上的低精度格式计算往往拥有更加高的算力,例如8-bit、4-bit的矩阵乘法算力通常是16-bit的2倍、4倍或更高。因此,在相同的时间内低精度格式往往比高精度要能处理更多的计算,大幅提高了大模型的整体计算效率。
指标 | FP16 | FP8 | FP4 |
内存占用 | 1x | 0.5x | 0.25x |
传输效率 | 1x | 2x | 4x |
硬件算力 | 1x | 2x | 4x+ |
表格1:低精度量化所带来的收益
低精度量化实现
以上介绍了低精度量化带给大模型的各种优势。然而,随着比特数量的减少会不可避免地带来精度上的损失。这是因为高比特格式中可表达的数值范围以及间隔无法在低比特格式中被表达出,因此带来潜在的模型效果下降,尤其是大数值的截断所带来的影响最为严重。提高低精度格式最常见的解决方法为通过使用缩放因子(Scaling Factor)来缩放数据范围,从而降低量化所造成的精度损失。
量化公式
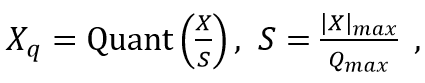
反量化公式
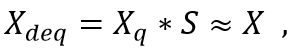
这里Quant为量化操作(数值截断和精度转换)、X为原始高精度数据、S为缩放因子、Qmax为目标低精度的最大值。该缩放方法通过找到数据中的绝对最大值,将原始高精度数据的范围归一化至目标低精度的最大值,来降低精度损失。
为了进一步降低量化对大模型所带来效果影响,业界使用了细粒度的缩放因子进行量化。例如DeepSeek V3 [2] 使用了分块量化(Block Scaling)的方案,成功训练出了第一个模型权重为FP8格式的大模型(在开源模型中)。该细粒度量化使用了1×128个中间激活数据为一组的量化,以及128×128个权重数据为一组的量化(如图1a所示)。

图1a) DeepSeek V3/R1模型中线性层前向(FWD)和激活反向(BPA)所使用的1×128 A矩阵和128×128 B矩阵的量化
这里对权重的量化为128×128一组的正方形是针对训练时的性能考虑。这是因为反向传播所进行的矩阵乘法的累加维度和前向相反(转置关系),因此前向和反向过程中均需要进行量化。例如,前向针对A量化、而反向针对A转置量化,这个过程也称之为重量化(Re-Quantization)。重量化会带来性能损失,并且需要存两份数据,如果使用了128×128则因其对称性即可解决这些问题。而中间激活难以进行128×128粒度的量化是因模型效果的考虑,毕竟token的组合非常之多(中间激活尺寸为token数×channel大小),不像模型权重是静态的数据。这就导致在计算权重梯度(等于中间激活转置乘以前一层的激活梯度)时需要1×128和128×1粒度的量化(如图1b所示)。
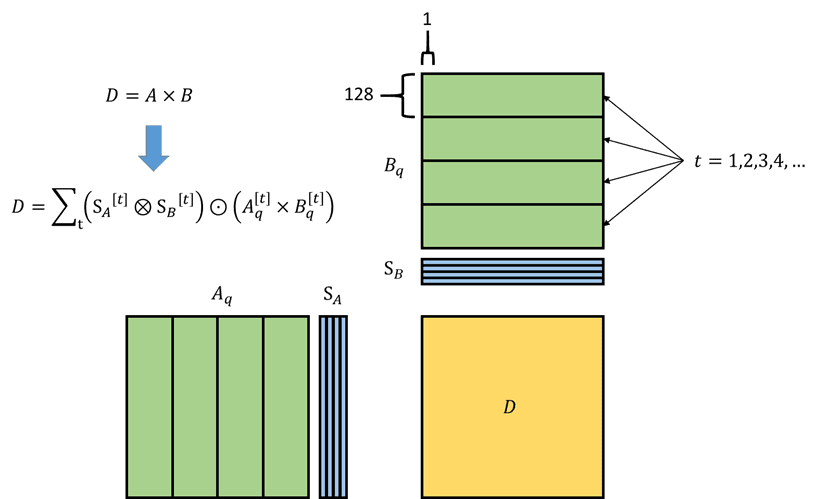
图1b) DeepSeek V3/R1模型中线性层权重反向(BPW)所使用的1×128 A矩阵和128×1 B矩阵的量化
虽然细粒度量化大幅降低了精度损失,然而却引入了更多的缩放因子,并且这些缩放因子的格式为高精度的FP32格式,减弱了低精度量化本身所带来的性能优势。因此,我们也可以对这些细粒度缩放因子进行量化,之后每一组低精度缩放因子会对应一个全局高精度的缩放因子。这种两级量化降低了细粒度缩放因子的存储问题,并且已经被应用在实际大模型部署中,例如在Llama.cpp这个开源项目中[3]。
指数细粒度FP4格式(MXFP4)
这是一种由Open Compute Project (OCP) 联盟所定义的一种细粒度FP4格式。其核心思想为采用细粒度的FP4量化,MXFP4为每32个元素组成一个数据块,以及对应每个数据块的一个纯指数8比特格式(UE8M0)的缩放因子——
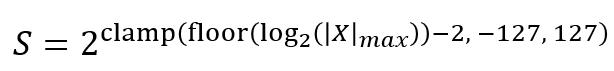
MXFP4采用的这种细粒度量化方式能大幅提升FP4的量化精度,并且平衡了硬件的高利用率。其所采用的8比特纯指数缩放因子不仅降低了存储空间需求和数据搬运量,还提供了对硬件友好的缩放运算方式(纯位移操作)。
除了MXFP4所定义的量化粒度(32)和缩放因子格式(UE8M0),业界和学术界也有使用过其他量化粒度(例如16、64、128等),以及其他缩放因子格式(INT6、INT8、FP8等)。最终会收敛至哪种形式估计还需要根据后续工作找到效果和效率之间最佳的平衡点。
目前,能原生态支持MXFP4精度(训练时线性层精度为A4W4)的开源大模型仅有OpenAI刚发布的GPT-OSS系列大模型(仅MoE层使用MXFP4精度)。可以预见未来会有更多的大模型支持原生态的FP4精度,虽然具体的缩放因子格式和颗粒度可能会不同于MXFP4。
异常值平滑处理(Outlier Smoothing)
细粒度量化的确在很大程度上能缓解低精度对模型效果的负面影响。然而,如果我们观察模型的中间激活分布可以发现该矩阵中的数值差异主要根据不同的channel来划分,而不在token维度上。
这带来了一大挑战,原因是中间激活的channel维度是矩阵乘法的累加维度,而之前介绍的细粒度量化在累加维度上是无法做到粒度为1的量化(因硬件中的张量核需要能一次性做大量的乘积累加(Dot Product)来保证高效矩阵乘法计算,因此需要大的累加维度)。这意味着如果一个数据块(例如128个数)中存在极个别的异常值(outlier),则它们的存在会极大影响该数据块的整体缩放,从而影响量化的精度。
针对这个问题诞生了平滑处理的方法,例如AWQ [4]、SmoothQuant[5]等,其核心思想为找到一个在累加维度粒度为1的向量来同时缩放模型的中间激活和权重,并且保证不会改变它们的矩阵乘法结果,也就意味着不需要进行“反量化”。具体为
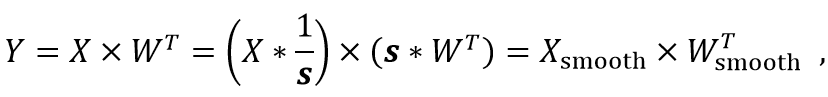
这里的s是一个在channel维度(累加维度)粒度为1的特殊“缩放因子”,其定义为
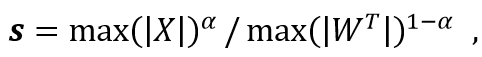
这里α控制对中间激活数据的平滑力度,其默认值为0.5,也可以每个线性层都不一样,具体根据后训练校准(PTQ)来选择。异常值平滑其实也不是免费的午餐,其最终是将量化的难度从中间激活转移到了模型权重中,只不过模型权重的数值分布通常比较均匀,不易受异常值所影响(如图2所示)。
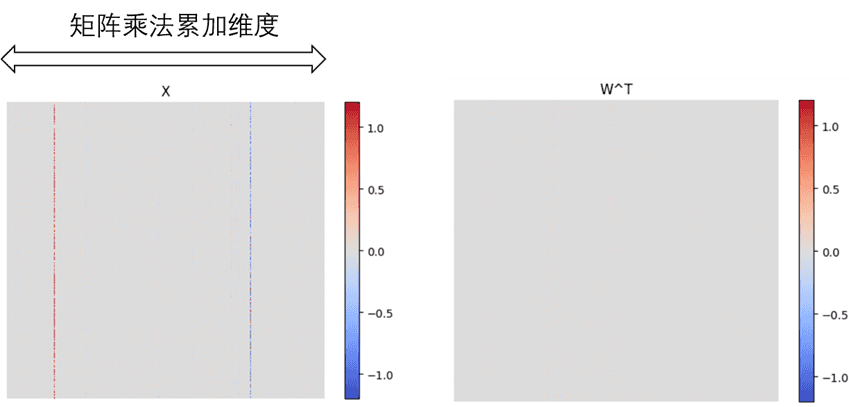
图2a) LLaMA模型中某一层的激活函数(X)和权重(W)的值范围,灰色部分表示其值接近于0。可以看出没经过平滑处理的激活函数在累加维度上有两组明显的异常值
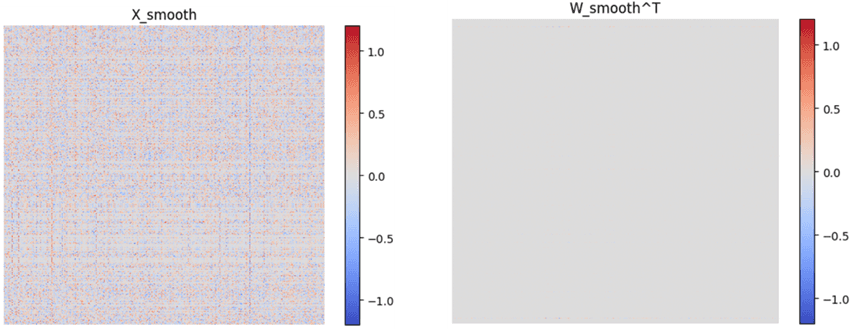
图2b) LLaMA模型中某一层经过平滑处理的激活函数(X_smooth)和权重(W_smooth)的值范围,灰色部分表示其值接近于0。可以看出经过平滑处理的激活函数在累加维度上的异常值幅度被大大降低了
之前展示的实验是根据16比特训练出来的模型做低精度量化时遇到的问题,但这些对于低精度格式为异常值的值对于16比特精度则不是问题。因此,这里有个猜想是如果模型本身就是低精度训练出来的,则可能不会出现这些异常值。因为在模型训练的过程中,数值的分布可能会适应当前使用的精度格式。因此,关于低精度预训练过的模型是否需要平滑处理的问题,可以期待后续技术发展能做解答。
低精度量化的近期发展
大模型的主要计算都来源于矩阵乘法,对精度的要求不像科学计算领域中需要求解线性方程或者逆矩阵等数值敏感的操作。因此,低精度量化不会过度影响大模型的预测能力。
在模型推理的场景中,低精度量化已是逐渐成熟的技术。除了DeepSeek V3/R1和Kimi-K2这类原生态支持FP8精度(训练时线性层精度为A8W8)的模型以外,其他模型也可以在VLLM、SGLANG等开源推理框架中进行低精度推理,包括Weight-only、Activation-Weight、Activation-Weight-KVCache的各种组合精度的量化 [5-9],甚至已经可以做到接近1比特的压缩 [10-12]。而大模型里的Attention算子仍然比较难支持低精度的量化,因为其对数值精度比线性层更为敏感。如想要保证精度损失在可接受范围内,低比特Attention需要进行额外的计算操作,包括在Q、K、V中加入累加维度的偏移项、Softmax的细粒度缩放、P×V中更高的累加精度等。通过这些手段可以将attention算子的精度降低至8比特[13,14]、甚至4比特[15]。在AI图片生成领域中,通过低秩分解(SVD)也已经能将模型的FP4量化做到精度几乎无损的效果,带来可观的性能加速[16],并且这项技术理论上也可以移植到AI视频生成这种推理速度极慢的场景中,从而缓解用户的等待。
在模型训练的场景中,因反向传播以及其他因素的影响,低精度训练仍是一件具有挑战的事情。目前,DeepSeek V3/R1和Kimi-K2(沿用了DeepSeek的结构)这两个模型使用了FP8细粒度的量化,成功地原生态支持FP8低精度(包括计算精度也是FP8)。随着更多芯片在硬件上开始支持4比特,例如FP4 E2M1的计算,针对FP4训练的方法也因此逐渐发展起来。通过一些技术手段,已经证明FP4精度下的模型训练是可以收敛甚至接近原始的BF16/FP16精度[17-22]。除了更细粒度的量化(例如16、32),其他技术手段包括梯度量化的随机舍入(Stochastic Rounding)、量化的反向函数近似、随机Hadamard转换来消除异常值等,均可提升FP4训练的收敛效果。
这里我们详细介绍其中几篇比较有代表性的FP4训练相关工作:
1)Oscillation-Reduced MXFP4 Training for Vision Transformers: arxiv.org/pdf/2502.20853
这篇论文虽然针对的是视觉领域的问题,但其方法对训练大语言模型也同样适用。这个工作的一大核心点是低精度模型训练需要进行重量化以及随机舍入来准确估计反向梯度:
模型前向

模型反向
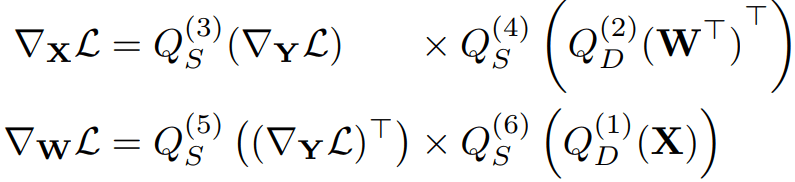
注意这里的两次量化之间存在反量化的过程,其中 Q(1)(3)(5)使用了1×32(per-token)的量化,Q(2)(4)(6) 使用了32×1(per-channel)的量化。下标D代表就近舍入(Round-to-Nearest)而S代表随机舍入,也就是根据数值在两点之间的距离存在对应的概率进行四舍或者五入。这是因为在前向过程中,我们希望使用最精准的低精度量化方法来近似高精度的数据,因此采用就近舍入的方式。然而,在进行反向求梯度做参数更新是对应前向量化的过程(就近舍入),如果再次使用就近舍入的方法来量化反向数据则会引入偏差。模型训练通常是批量更新参数,也因此引入了统计的概念。而随机舍入在统计上是无偏的(unbiased),因此更适合在反向中使用。这里其实涉及到前向误差(Forward Error)和反向误差(Backward Error)的理论分析,然而篇幅有限就不在此深入展开了。此外,重量化的引入也是为了降低偏差。
因为该工作开源了实现代码,我们可以做一个复现实验来对比FP4和BF16的训练收敛效果。可以从图3中看出FP4训练是可收敛的,意味着损失函数呈下降的趋势。然而其收敛的速度与BF16相比仍有差距。因此,FP4的训练很可能需要额外引入其他手段来提升精度,从而赶上16比特格式的训练效果。
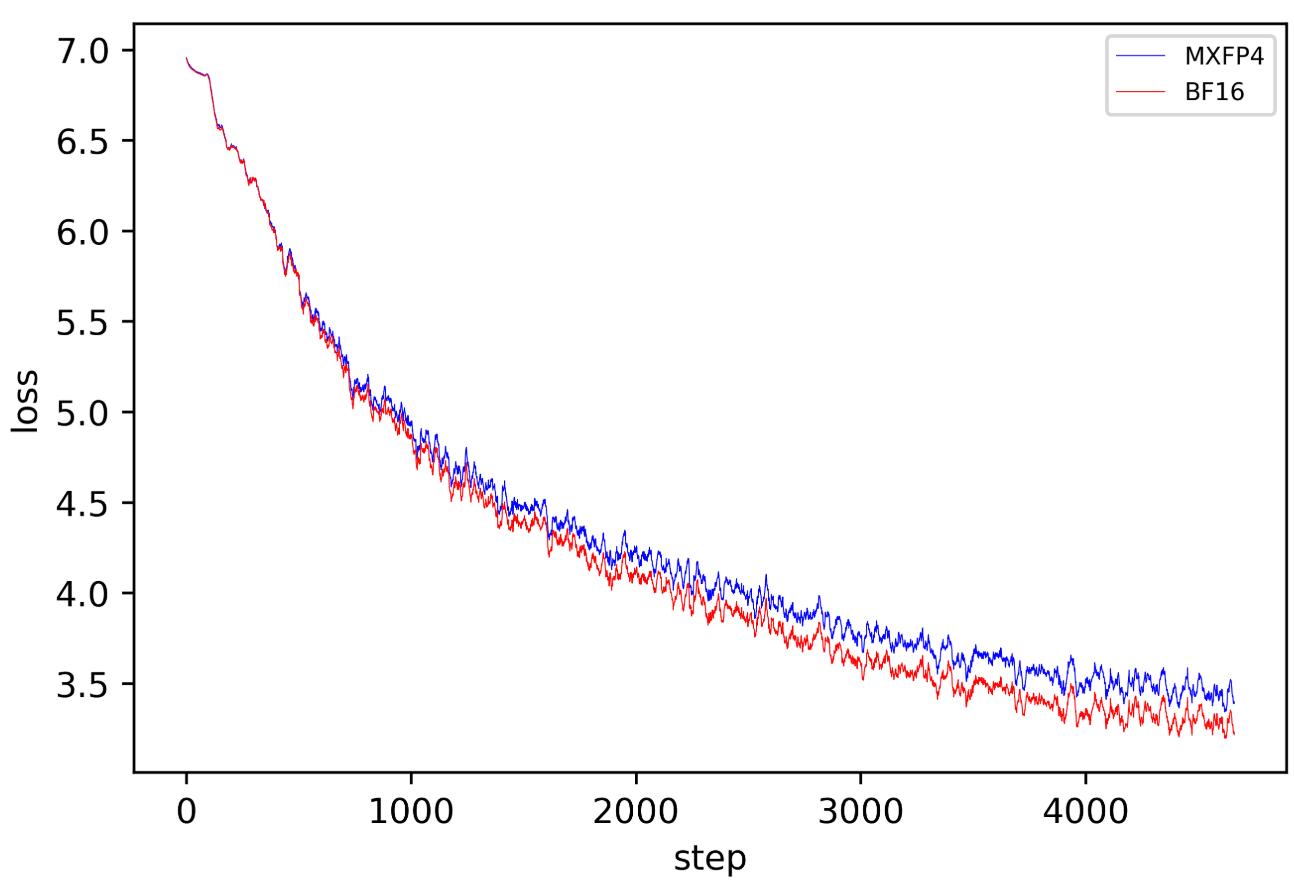
图3:针对 1)所提出的量化方法进行的FP4训练的实验复现
2)FP4 All the Way: Fully Quantized Training of LLMs: arxiv.org/pdf/2505.19115
这项工作的采用了类似1)的方法进行前向和反向的FP4量化,不过应用在了大语言模型的场景中。此外,从其给出的实验结果(图4)我们可以看到FP4和BF16的收敛差距与图3类似,这里给出的一种解决方法为,在训练的最后一小阶段中的反向过程中采用了BF16的格式就可以弥补之前纯FP4格式训练所造成的差距。整体来说,在训练的绝大部分过程中使用FP4进行高效计算,但在占比很小的训练后期提高反向的精度来达到纯16比特训练的效果。
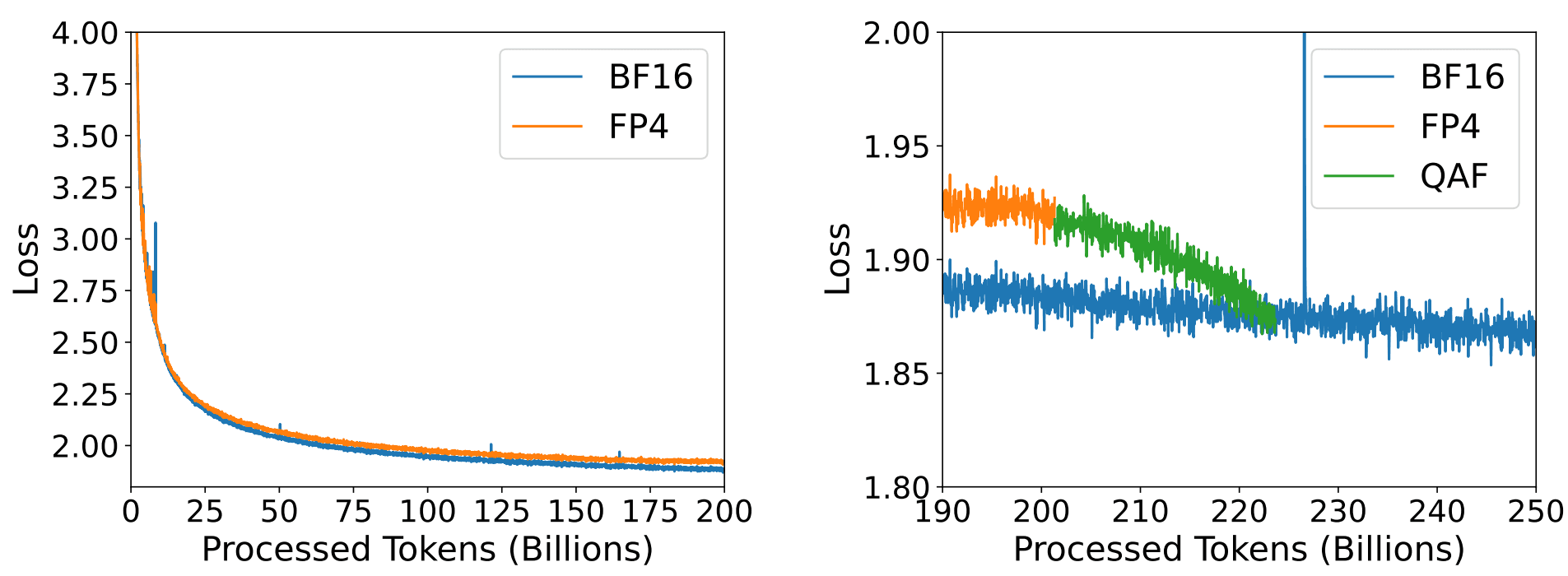
图4:FP4与BF16的训练收敛对比。该图来源于2)的文章
3)Optimizing Large Language Model Training Using FP4 Quantization: arxiv.org/pdf/2501.17116
该论文提出了两个技术点来让FP4训练的收敛效果与16比特训练非常接近。首先,从高精度量化至低精度这个量化的操作是不可微分的,其导数在几乎所有点上均为零。因此,在以往的低精度训练中都假设反向传播是针对量化前的高精度张量而不是量化后的低精度张量,从而引入不小的误差,特别是在4比特这种高压缩的场景中。在1)和2)的工作中使用了随机舍入和重量化来纠正偏差,而这里3)则采用了可微函数的估计方式来近似量化这个过程。假设量化操作Quant可以被一个可微的函数f近似,文章中使用了以下定义:
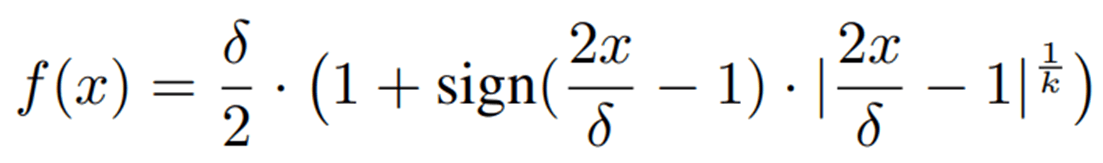
因此其导数为:
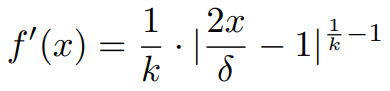
这里k的值可以根据实验调整,文章中默认为5, δ 则是量化的间隔(Quantization Interval)。实际训练中,前向还是使用正常的量化操作,而反向时则使用了函数导数f'来近似梯度。
最后,为了进一步缩小FP4量化的精度损失,该工作还提出了将异常值从原始张量中分离,进行稀疏高精度矩阵乘法的方法来减少计算误差:
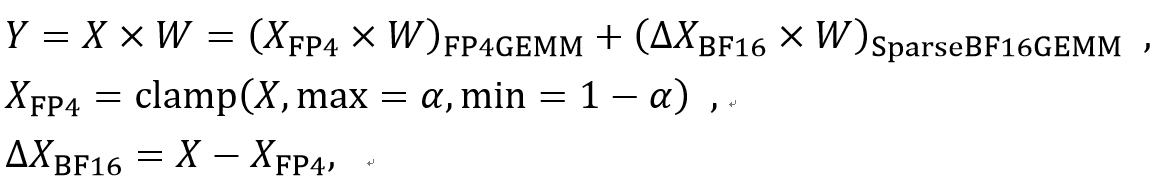
这里α=0.99或者0.999为截断的最大值分位数。实际训练中,ΔXBF16处于高度稀疏的状态,文章中提到该张量只拥有0.2%~2%非零元素。因此,理论上BF16的稀疏矩阵乘法所带来的计算量很小。
处于高度稀疏的状态,文章中提到该张量只拥有0.2%~2%非零元素。因此,理论上BF16的稀疏矩阵乘法所带来的计算量很小。

图5:FP4的基础实现和使用文章中方法的FP4训练与BF16的训练收敛对比。该图来源于3)的文章
4)Training LLMs with MXFP4: arxiv.org/pdf/2502.20586
这项工作提出了使用细粒度的随机哈达玛变换(Random Hadamard Transform,RHT)来减少异常值出现的概率从而降低FP4量化的精度损失,以及细粒度(与量化粒度一致)的哈达玛变换实现,帮助降低计算量从而提高性能。其具体转换为:
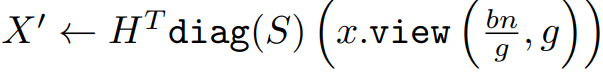
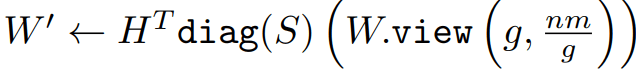
这里X和W分别为b×n的中间激活和n×m的模型权重,H为哈达玛矩阵,S为值是+1或-1的随机向量,g为哈达玛变换的粒度。例如,与MXFP4量化粒度相同的情况下为g=32。这里利用了哈达玛矩阵H和 diag(S)均为正交矩阵的属性(A×A^T=I),因此矩阵乘法X×W与X'×W'的结果在理论上相等。
在低精度量化的场景中使用随机哈达玛变换的原因是,哈达玛转换本身可以将原始数据中的异常值(高能量数值)扩散至其他值中,使得整体系统的能量分布更加均匀,同时保持系统的整体能量不变(L2Norm-invariant),也就是说哈达玛变换起到了一种数据平滑的效果。随机哈达玛变换(RHT)在此基础上添加的随机性可以更大概率地扩散异常值的能量(通过破坏哈达玛矩阵的基与某些数据过于关联从而造成能量的集中所导致的异常值扩散失败)。此外,将随机哈达玛变换的粒度变小可以降低该变换的计算量,然而也会降低RHT在扩散异常值能量上的能力,所以这也是一种性能和效果的取舍。最后,这里的随机哈达玛变换需要在高精度的计算格式,例如FP32中进行。因此,该算子的优化也颇具挑战。
关于细粒度随机哈达玛变换对于FP4训练的影响,可以通过图6看到,使用了随机哈达玛变换的FP4训练拥有几乎与BF16训练相同的收敛效果,尤其是当模型的参数规模变大。
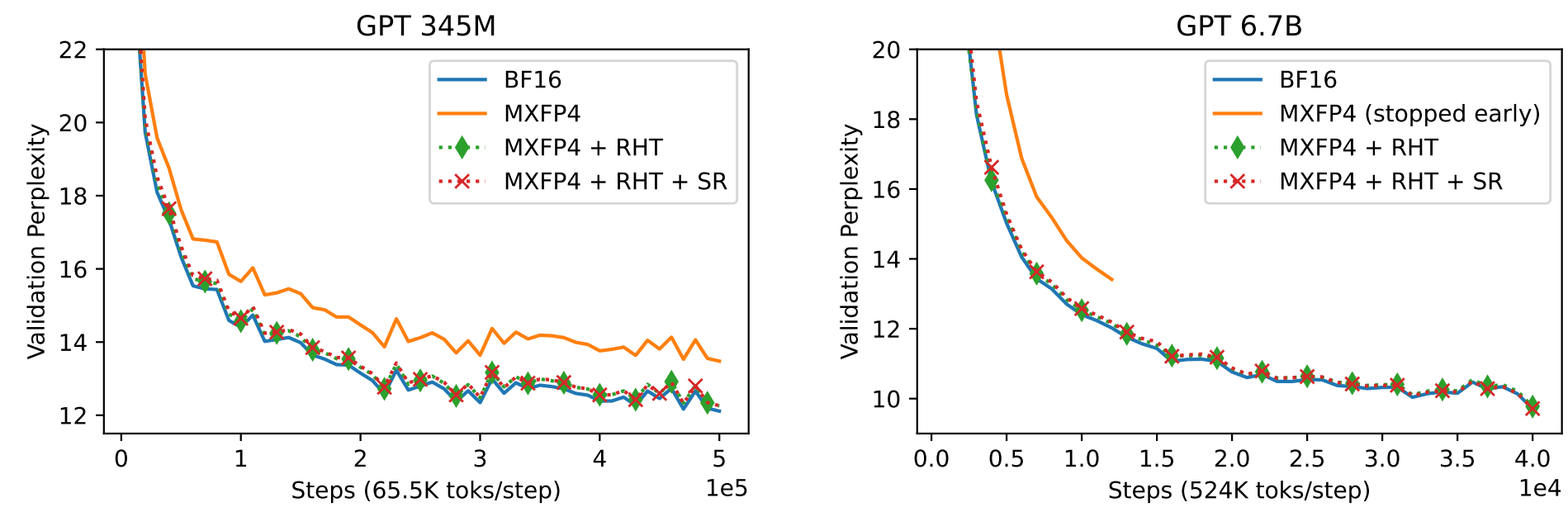
图6:FP4的基础实现和使用文章中包括随机哈达玛转换方法的FP4训练与BF16的训练收敛对比。该图来源于4)的文章
通过分析以上几项工作,我们可以得到基于现有FP4训练进展的结论:
1,FP4训练是可以收敛的,然而基础的FP4实现会比BF16训练的收敛速度慢;
2,FP4训练需要额外的计算来弥补与16比特训练的收敛差距(例如,训练最后阶段采用BF16精度的反向过程、BF16精度的异常值和权重的矩阵乘法、随机哈达玛变换来弱化异常值等方法);
3,OpenAI开源的GPT-OSS系列大模型在FP4量化中也相当保守,只量化了对精度不敏感的专家线性层,其他组件仍然保持BF16精度格式。此外,OpenAI似乎并未公开其训练细节。因此,其专家线性层的反向计算精度也仍然未知。
总 结
在AI领域中,特别是大模型的场景下,模型普遍对数值精度不敏感,不像HPC领域中需要FP64甚至更高的精度格式。从历史经验来看,模型的参数量规模远比高精度带来的收益要大,这一点在如今混合专家大模型的时代得到了很好的验证,包括目前几乎所有的主流开源大模型DeepSeek-R1 671B、MiniMax-M1 456B、Kimi-K2 1T、Qwen3-Coder 480B、GLM-4.5 355B、GPT-OSS 120B等均采用了MoE的结构。而模型参数量越大通常对低精度量化的容忍度越高 [23,24],因此针对超大规模模型的低精度量化往往能在效果损失很小的情况下带来巨大的性能收益。而效率的大幅提升则意味着各种开销,例如时间成本、数据存储需求等,均会大幅降低。因此,当硬件开始支持更高效率的计算格式时,开发人员就会想办法利用这些新的特性,尽可能地将硬件的性能利用满。
最后,随着低精度训练方法的成熟和更多芯片在硬件上对低比特格式的支持,大模型的训练时间将大幅缩短。这将催生更大、能力更强的模型,支持更长的token序列并提供更快的响应。此外,低精度计算及其他性能优化方法,例如近乎无损模型效果的启发式稀疏,不仅能显著提升大语言模型等文本生成任务的效率,还能大幅改善多模态领域,例如目前响应速度极慢的AI视频生成、世界模型等场景的生成效率。而这些跨模态领域的发展可以帮助人类更快地获得通用人工智能。
参考文献
[1] DeepSeek-V2: A Strong, Economical, and Efficient Mixture-of-Experts Language Model. https://arxiv.org/pdf/2405.04434
[2] DeepSeek-V3 Technical Report. https://arxiv.org/pdf/2412.19437v1
[3] llama.cpp: https://github.com/ggml-org/llama.cpp
[4] AWQ: ACTIVATION-AWARE WEIGHT QUANTIZATION FOR ON-DEVICE LLM COMPRESSION AND ACCELERATION. https://arxiv.org/pdf/2306.00978
[5] SmoothQuant: Accurate and Efficient Post-Training Quantization for Large Language Models. https://arxiv.org/pdf/2211.10438
[6] GPTQ: ACCURATE POST-TRAINING QUANTIZATION FOR GENERATIVE PRE-TRAINED TRANSFORMERS. https://arxiv.org/pdf/2210.17323
[7] SpinQuant: LLM quantization with learned rotations. https://arxiv.org/pdf/2405.16406
[8] QSERVE: W4A8KV4 QUANTIZATION AND SYSTEM CO-DESIGN FOR EFFICIENT LLM SERVING. https://arxiv.org/pdf/2405.04532
[9] COMET: Towards Practical W4A4KV4 LLMs Serving. https://arxiv.org/pdf/2410.12168
[10] BitNet: Scaling 1-bit Transformers for Large Language Models. https://arxiv.org/pdf/2310.11453
[11] The Era of 1-bit LLMs: All Large Language Models are in 1.58 Bits. https://arxiv.org/pdf/2402.17764v1
[12] OneBit: Towards Extremely Low-bit Large Language Models. https://arxiv.org/pdf/2402.11295v3
[13] SAGEATTENTION: ACCURATE 8-BIT ATTENTION FOR PLUG-AND-PLAY INFERENCE ACCELERATION. https://arxiv.org/pdf/2410.02367
[14] SageAttention2: Efficient Attention with Thorough Outlier Smoothing and Per-thread INT4 Quantization. https://arxiv.org/pdf/2411.10958
[15] SageAttention3: Microscaling FP4 Attention for Inference and An Exploration of 8-bit Training. https://arxiv.org/pdf/2505.11594
[16] SVDQUANT: ABSORBING OUTLIERS BY LOW-RANK COMPONENTS FOR 4-BIT DIFFUSION MODELS. https://arxiv.org/pdf/2411.05007
[17] Oscillation-Reduced MXFP4 Training for Vision Transformers. https://arxiv.org/pdf/2502.20853
[18] Optimizing Large Language Model Training Using FP4 Quantization. https://arxiv.org/pdf/2501.17116
[19] Towards Efficient Pre-training: Exploring FP4 Precision in Large Language Models. https://arxiv.org/pdf/2502.11458
[20] Training LLMs with MXFP4. https://arxiv.org/pdf/2502.20586
[21] Quartet: Native FP4 Training Can Be Optimal for Large Language Models. https://arxiv.org/pdf/2505.14669
[22] FP4 All the Way: Fully Quantized Training of LLMs. https://arxiv.org/pdf/2505.19115
[23] Evaluating Quantized Large Language Models. https://arxiv.org/pdf/2402.18158
[24] SCALING LAWS FOR MIXED QUANTIZATION. https://arxiv.org/pdf/2410.06722